- 4.1. Herkunft, Definition und Charakterisierung
- 4.2. Normalspannungseffekte
- Weissenberg-Effekt
- Quelleffekt , Sekundärströmungen
- Strangschwellen
- 4.3. Ermittlung von Normalspannungsdifferenzen
- Normalspannungsmessungen
- Ableitung der Normalspannungen über andere Größen
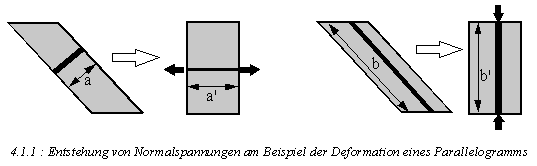
Die vorangegangenen Abschnitte gingen davon aus, daß durch eine Scherdeformation nur Schubspannungen im Material erzeugt werden. Bei viskoelastischen Materialien, also insbesondere Polymeren, werden bei Scherung auch Normalspannungskomponenten hervorgerufen. Diese wirken zusätzlich zum hydrostatischen Druck und sind zumeist für die Raumrichtungen verschieden. Bild 4.1.1 zeigt am Beispiel eines Parellelogramms diesen Sachverhalt. Wird durch eine oben angreifende und nach rechts wirkende Kraft das Parallelogramm in die Form eines Rechtecks überführt, so kommt es zu einer Dehnung bzw. Zugbeanspruchung der Materialschichten in Richtung der Deformationskraft (a'>a) und zu einer Stauchung bzw. Druckbeanspruchung in Richtung des Deformationsgradienten (b'<b).

Diese scherinduzierten Spannungen werden in Form der Normalspannungsdifferenzen N1 und N2 beschrieben.
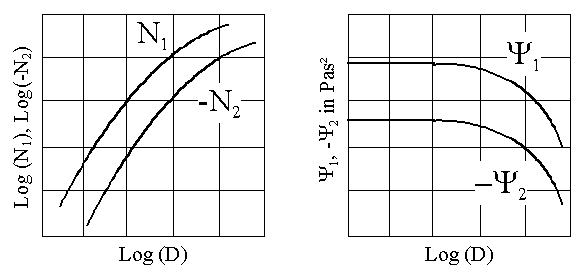
Die Differenzenbildung erfolgt dabei aus dem Grunde der Eliminierung des isotropen, statischen Druckanteils. Definitionsgemäß bezeichnet x die Richtung der Bewegung und y die Richtung des Gradienten, während z die indifferente Richtung darstellt. Wie im obigen Beispiel beschrieben und anhand von Abb. 4.1.2 unterstrichen, kommt es in den meisten Materialien durch Scherung zu einer Zugbeanspruchung in Strömungs- und zu einer Druckbeanspruchung in Gradientenrichtung. Dies führt zu einer positiven ersten bzw. einer negativen zweiten Normalspannungsdifferenz. Dabei ist N1 meist um einige Größenordnungen größer als N2. Der Anstieg der Funktionen N1(D) und N2(D) ist in der logarithmischen Darstellung nach Abb. 4.1.2 für kleine Scherraten konstant und zeigt eine Proportionalität von Normalspannungsdifferenzen und Quadrat der Scherate an. Die entsprechenden Proportionalitätsfaktoren sind die Normalspannungskoeffizienten Y1 und Y2 :
Das Auftreten von Normalspannungen kann zu Effekten führen, die aus dem Verhalten Newtonscher Fluide nicht bekannt sind oder diesem widersprechen. Einige dieser Effekte sollen folgend vorgestellt werden. Dabei wird zumeist nur eine populistische Erklärung gegeben und weniger auf die analytische Formulierung Wert gelegt..
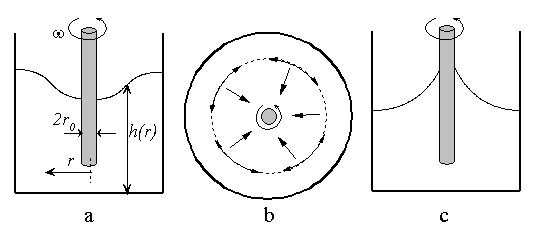
Wird ein rotierender Stab in ein großes Gefäß gefüllt mit einer Newtonschen Flüssigkeit gebracht, so bildet sich bei geeignet hohen Drehzahlen eine Trombe heraus (Bild 4.2.1). Diese Absenkung des Flüssigkeitsspiegels in Richtung Rotationsachse wird durch die wirkenden Radialkräfte verursacht. Wird statt einer newtonschen Flüssigkeit ein viskoelastisches Fluid eingesetzt, so kommt es zur Ausbildung von Normalspannungen, insbesondere einer Zugspannung in Strömungsrichtung. Stellt man sich diese Zugspannung als einen gespannten Gummi-Ring vor, so wird eine resultierende Kraftwirkung in Richtung Rotationsachse deutlich. Ist diese Kraftwirkung größer als die ihr entgegengesetzt wirkende Radialbeschleunigung, so kommt es zur Anhäufung von Material und damit zur Anhebung des Flüssigkeitsspiegels in Richtung der Rotationsachse (rotierender Stab). Dieser Klettereffekt wird auch als Weissenberg-Effekt bezeichnet.
Eine Beschreibung der Weissenberg-Effektes kann durch Bildung der Kräftebilanzen in analytischer Form erfolgen (Siehe G.Böhme ,"Strömungsmechanik nicht-newtonscher Fluide", B.G. Teubner, Stuttgart, 1981). Aus dem danach ableitbaren radialen und axialen Druckverlauf ergibt sich für die freie Oberfläche in einem unendlich großen Reservoir des Fluids ein gekrümmter Verlauf, der nach :
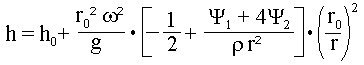
beschrieben werden kann. Hierbei bedeuten h0 die Füllhöhe bei gleichmäßigem Niveau, r0 und w den Radius bzw. die Winkelgeschwindigkeit des rotierenden Stabes sowie r die Dichte des Fluids. Der entscheidende Term für die Absenkung (normale Trombe) oder Anhebung (Weissenberg-Effekt) des Oberflächenspiegels ist derjenige in den rechteckigen Klammern. Ohne bzw. bei geringen Normalspannungseffekten ergibt sich ein negativer Klammerausdruck entsprechend einer Senkung des Spiegels. Der Weissenberg-Effekt stellt sich dann ein, wenn der zweite Term größer als 0,5 wird. Dazu ist jedoch zunächst ein positiver Normalspannungsausdruck (Zähler des 2.Terms) notwendig. Desweiteren muß der Stabradius kleiner als der Grenzradius sein, der sich durch Nullsetzen des Klammerausdrucks ergibt ( r* = [ 2·(Y1 + 4·Y2) / r]^½ ). Bei der Anwendung der Beziehungen ist zu beachten, daß hier ein unendliches Fluidreservoir (Potentialwirbel) vorausgesetzt wurde. Für reale Gefäße mit endlichen Abmessungen sind einige zusätzliche Effekte zu beachten. Dazu gehört die Erfüllung der Massebilanz, die beispielsweise bei einer Absenkung des Fluidspiegels in Stabnähe eine Anhebung in den Außenzonen erfordert. Ein weiterer Fakt sind die Reibungskräfte zur Gefäßwandung, die einer Formulierung als Potentialwirbel entgegenwirken. Zu den zusätzlichen Effekten von Normalspannungen in begrenzten Geometrien gehört auch die Ausbildung von Sekundärströmungen, für die der folgend behandelte Quelleffekt ein Beispiel darstellt.
Quelleffekt , Sekundärströmungen
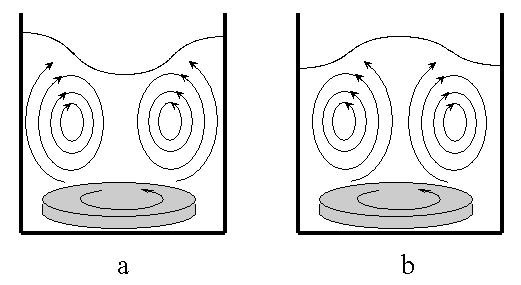
Beim Einsatz eines rotierenden Stabes kommt es zur Ausbildung eines Druckgradienten in radialer Richtung als Folge von Radialbeschleunigung bzw. Normalspannungen. Steckt der Stab tief im Fluid, so wirkt der Gradient über die gesamte Länge des Stabes und kann daher nur durch ein Anpassung der Flüssigkeitsoberfläche ausgeglichen werden. Im Gegensatz dazu kann der Druckgradient bei einem nur eingetauchter Stab oder eine rotierende Scheibe (Bild 4.2.2) durch eine Strömung ausgeglichen werden. Diese, der viskosen Strömung überlagerten, Strömung wird als Sekundärströmung bezeichnet. Auch hier entscheidet die Dominanz von Radialbeschleunigung oder Normalspannung über die Qualität der Strömung. Dominiert die Normalspannung, so wird in Nähe des rotierenden Teils eine Strömung in Richtung Mitte ausgelöst. Bei einer am Boden befindlichen, rotierenden Scheibe resultiert hieraus eine in der Mitte emporsteigende Strömung, die infolge des Impulsaustausches bei der Umlenkung zur oberen Querströmung zu einem Anstieg der Flüssigkeitsoberfläche in der Mitte des Behälters führt (Quelleffekt). Im Gegensatz dazu ist in einem Newtonschen Liquid die klassische Trombenbildung mit nach außen ansteigendem Flüssigkeitsspiegel zu beobachten.
Eine Ermittlung der Höhe im Zentrum ist nach einer Beziehung möglich, die der für den Weissenberg-Effekt (siehe oben) weitgehend entspricht (G.Böhme ,"Strömungsmechanik nicht-newtonscher Fluide", B.G. Teubner, Stuttgart, 1981):
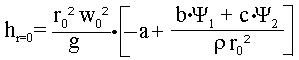
Hierbei bezeichnen a,b und c Konstanten, die die Geometrie von Scheibe und Behälter beschreiben.
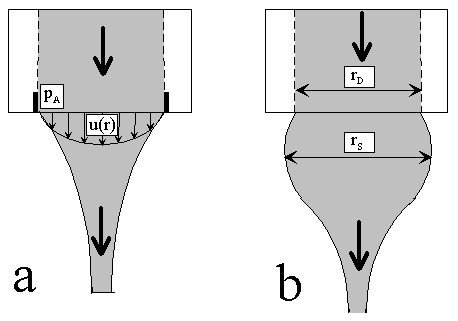
Betrachtet sei der Freistrahl eines Fluids beim Austreten aus einem kreisrunden, senkrechten Rohr (Bild 4.2.3). Bei einem Newtonschen Medium kommt es infolge der Schwerkraft zu einer Beschleunigung des Fluids und somit einer wachsenden Geschwindigkeit mit steigender Entfernung vom Austritt. Aus Gründen der Masseerhaltung muß bei inkompressiblen Medien der Geschwindigkeitszuwachs durch eine Verringerung des Querschnitts aufgefangen werden, so daß sich ein verengender Strahl nach Bild 4.2.3 a einstellt. Auch bei einem viskoelastischen Fluid wirkt die Schwerkraft in der oben angegebenen Art. Zusätzlich wirken durch die Scherdeformation in Nähe des Austritts eine Zugspannung in Strömungsrichtung und eine Druckspannung quer dazu. Dies führt zu einer Aufweitung des Strahles gegenüber dem Düsendurchmesser. Dieser Effekt wird auch als Strang- oder Extrudatschwellen und die resultierende Strangform als Zwiebelbildung bezeichnet (Bild 4.2.3 b).
Das maximale Aufweitungsverhältnis des Strahles kann durch Bilanzierung gewonnen werden (G.Böhme, "Strömungsmechanik nicht-newtonscher Fluide", B.G. Teubner, Stuttgart, 1981) und ergibt sich zu:
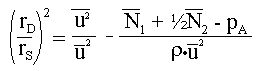
Hierbei bedeuten u die axiale Geschwindigkeit über dem Düsenradius, pA den Austrittsdruck (Bagley-Druck, siehe auch Normalspannungsmessung) und r die Dichte des Fluids. Die angezeigten Mittelungen erfolgen über dem Düsenaustritt. Für verschiedene Annahmen (z.b. voll ausgebildete Poiseuille-Strömung, kein Austrittsdruck) kann eine Vereinfachung der Gleichung erfolgen. Insbesondere läßt sich ein kritischer Düsendurchmesser r* = [ 12·(2·Y1 + Y2) / r]^½ ermitteln, dessen Unterschreitung für eine Aufweitung des Stranges Voraussetzung ist.
4.3. Ermittlung von Normalspannungsdifferenzen
Normalspannungen, deren Differenzen bzw. Koeffizienten können über direkte Messungen ermittelt oder aber über andere Meßgrößen abgeleitet bzw. abgeschätzt werden. Im Folgenden seien zunächst die Möglichkeiten zur direkten Messung vorgestellt um später auf die Beziehungen der Normalspannungsdifferenzen und anderer rheologischer Größen einzugehen.
Die Messung von Normalspannungen kann einerseits über die direkte Erfassung von Drücken bzw. Kräften und andererseits über die Quantifizierung von Normalspannungseffekten erfolgen. Zur letzteren Gruppe gehören insbesondere die Ermittlung der Steighöhe bei Weissenberg-oder Quelleffekt und die Auswertung des Strangschwellens (Extrudatschwellens) bei einer Düsenströmung.. Nach entsprechenden Beziehungen kann so eine Aussage über die Normalspannungsdifferenzen gewonnen werden.
Für die Messung von Drücken bzw. Kräften mit Hinblick auf die Ableitung von Normalspannungsdifferenzen eignen sich unter den Rotationsrheometern insbesondere Kegel-Platte-Systeme. Abb. 4.3.1 zeigt einige Möglichkeiten zur Ermittlung des Druckverlaufes entlang des Radius. Neben Druckaufnehmern (z.B. Piezo-Elementen) können auch Kapillaren eingesetzt werden. Der gemessene Druck entspricht der Normalspannung tyy und zeigt einen linearen Verlauf über dem natürlichen Logarithmus des Radius. Der Anstieg entspricht dabei genau dem Term -(N1+2N2). Unter Vernachlässigung der Oberflächenspannung kann der gemessene oder extrapolierte Druckwert an der Außenkante (r = R) der zweiten Normalspannungsdifferenz gleichgesetzt werden. Damit ist die erste Normalspannungsdifferenz aus dem Anstieg der Geraden extrahierbar.

Die Ableitung der Normalspannungsdifferenzen kann nicht nur über den radialen Druckverlauf sondern auch über die integrale Normalkraft Fz (siehe Bild 4.3.1) erfolgen. Dieses Prinzip nutzen die meisten angebotenen Rotationsrheometer mit Normalspannungsmessung. Der Zusammenhang von erster Normalspannungsdifferenz und integraler Normalkraft ergibt sich durch Integration der Normalspannungen über dem Radius zu:
Der angegebene Zusammenhang gilt unter Vernachlässigung der Radialbeschleunigung des Liquids. Letztgenannter Effekt führt zu einem Unterdruck im Meßraum, der zur gemessenen Normalkraft beiträgt. Daher ist zur Ableitung der ersten Normalspannungsdifferenz eine Korrektur der Normalkraft erforderlich
Hierbei bedeutet r die Dichte des untersuchten Materials und w die Winkelgeschwindigkeit. Neben dem Unterdruck kann durch die Radialbeschleunigung eine Sekundärströmung ausgelöst werden, die ebenfall zur gemessenen Normalkraft beitragen kann. In den meisten Fällen reicht jedoch die oben angegebene Korrektur aus.
Prinzipiell ist eine Messung der Normalspannungsdifferenzen auch mit anderen rotierenden Meßgeometrien möglich. Hierbei treten jedoch meist Probleme hinsichtlich der Erfassung der Kräfte oder in der Ermittlung der einzelnen Größen auf. So kann in einem Platte-Platte-System durch Messung der Normalkraft zwar die Differenz N1-N2, jedoch nicht die beiden Einzelbeiträge N1 und N2 abgeleitet werden. In einem koaxiale Zylindersystem ist zwar die Ableitung von N1 möglich, jedoch ist hierfür eine Messung der radial auf die Zylinder wirkenden Drücke notwendig. Was für den stationäre Zylinder noch möglich, wird für den rotierenden Zylinder äußerst kompliziert. Daher empfielt sich für die Normalspannungsmessung in rotierenden Systemen immer die Kegel-Platte-Geometrie.
Neben den rotierenden Systemen sind auch Druckrheometer für die Erfassung von Normalspannungsdifferenzen insbesondere bei hohen Scherraten geeignet. Neben der Auswertung des Extrudatschwellens besteht die Möglichkeit der Messung des Druckverlaufes entlang einer Düse bzw. eines Schlitzes mittels Druckaufnehmern (Bild 4.3.2). Durch Extrapolation der Druckkurve auf die Endlänge L , kann der sogenannte Austrittsdruck pA ermittelt werden. Wird der Austrittsdruck als auch die Wandschubspannung als Funktion der Scherrate (Durchfluß) ermittelt, kann die erste Normalspannungsdifferenz berechnet werden (hier für Schlitzrheometer mit linearer Extrapolation des Austrittsdruckes):
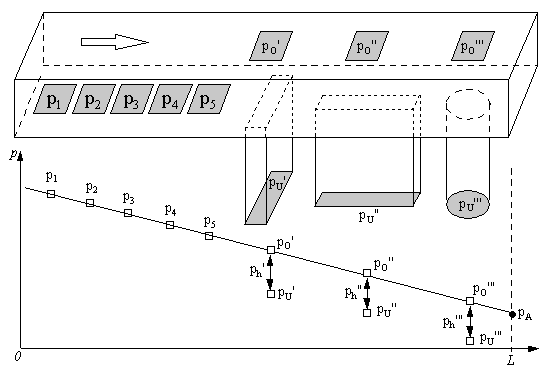
Die Ableitung des Austrittsdruckes, inbesondere auch die Extrapolation, stellen massive Fehlerquellen dieser Messung dar. Prinzipiell kann dieser Druck auch aus Druckverlustmessungen für verschiedene Düsen- bzw. Schlitzlängen ermittelt werden, indem eine Extrapolation auf verschwindende Düsenlänge durchgeführt wird (Bagley-Plot). Eine bessere und genauere Möglichkeit der Messung von Normalspannungsdifferenzen in Druckrheometer bietet der Einsatz von Druckstutzen (Bild 4.3.2), der sowohl bei Kapillaren als auch Schlitzen möglich ist. Dabei wird der Differenzdruck im Stutzen und dem Stutzen gegenüber ermittelt und zur Ableitung der Normalspannungen genutzt. Je nach Form des Druckstutzens ergeben sich folgende Beziehungen:
Querschlitz : N1=2 · ph' · d( ln ph' ) / d( ln tw) Längsschlitz : N2= -ph'' · d( ln ph'' ) / d( ln tw) Kreisförmig : N1-N2 = 3 · ph''' · d( ln ph''' ) / d( ln tw)
Ableitung der Normalspannungen über andere Größen
Neben der direkten Messung kann eine Abschätzung der Normalspannungen über andere Meßgrößen erfolgen. So gilt zum Beispiel folgender Zusammenhang zwischen dem ersten Normalspannungskoeffizienten bei einer Scherrate D und dem aus oszillatorischen Messungen abgeleiteten Speichermodul G'(w):
Diese Beziehung ist jedoch nur für sehr kleine bzw. verschwindende Scherraten bzw. Frequenzen gültig.
Eine Möglichkeit zur Berechnung der ersten Normalspannungsdifferenz bietet auch die Messung der Schubspannung nach einem Schersprung Dg (Lodge-Meissner-Beziehung):
Zur Ableitung der Schergeschwindigkeitsfunktion des ersten Normalspannungskoeffizienten kann auch der zeitliche Verlauf von N1 für verschwindende Schergeschwindigkeit genutzt werden (Spiegelrelation) :
Der Koeffizient k ist eine Stoffkonstante, die im wesentlichen zwischen 2 und 4 varriert. Ist jene Konstante bekannt, so ist auch eine Ableitung von Y1(D) aus der Funktion der stationären Scherviskosität h(D) möglich (W. Gleissle ; Rheologica Acta, Vol. 21(1982), S. 484 ) :
Dabei erfolgt die Summation der Viskositätsfunktion ausgehend von Di= ¥ bis zum Wert D